大阪大学医学部 Python会

Now is better than never.

線形混合効果モデル

2020-04-08(Wed) - Posted by 竹内 in 技術ブログ    tag:Statistics

Contents

    経時測定データ解析

    複数の対象者に対して、ある反応変数を時間の経過とともに繰り返し測定したデータを、経時測定データ（longitudinal data）という。経済学分野では、パネルデータ解析として知られている。

    経時測定データ解析の特徴

    • 個体間誤差だけでなく、個体内誤差も考慮する必要がある。
    • 個体内の各観測値は独立ではない為、相関を考慮する必要がある。
    • ランダム化比較試験 (RCT) では個体毎の測定回数は同じであることが多いが、観察研究では個体毎に測定回数がバラバラであることが多い。

    線形混合効果モデル

    • \(N\)人 (\(i=1, 2, \cdots, N\))の被験者を対象とする。
    • \(i\) 番目の被験者は \(n_i\) 回測定されるとする。
    • \(Y_{ij}\) は、\(i\) 番目の被験者の、\(j\) 番目 (\(j=1, 2, \cdots, n_i\)) の時点における被説明変数とする。
    • この時、線形混合モデルはベクトル表記にて、以下のように表される。
    $$ \boldsymbol{Y}_i = X_i \boldsymbol{\beta} + Z_i \boldsymbol{b}_i + \epsilon_i $$

    ただし、\(\boldsymbol{\beta}\)は固定効果、\(\boldsymbol{b}_i\)はランダム効果（変量効果）を表すベクトルとした。また、\(X_i, Z_i\)は計画行列である。

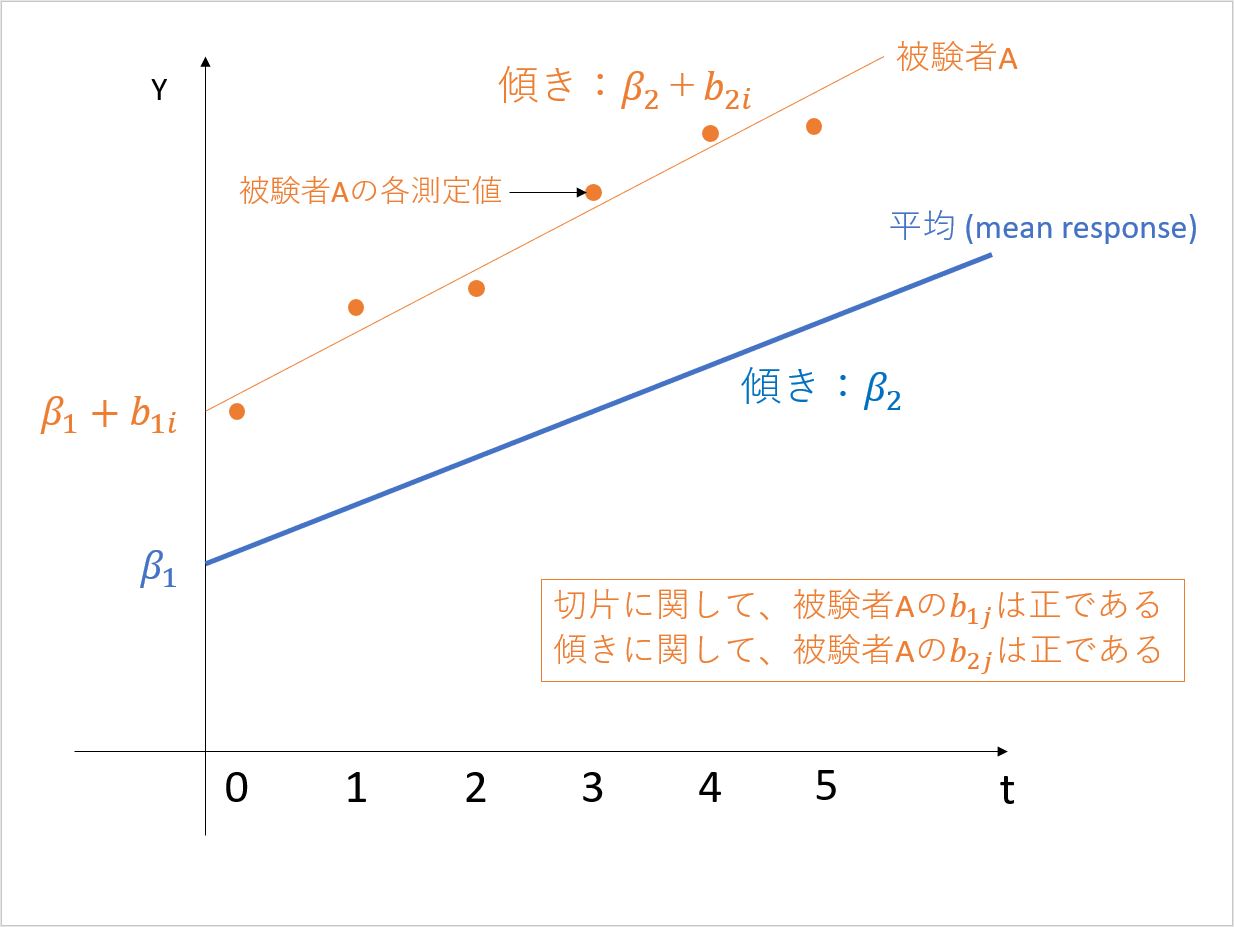
    ベクトル表現を書き下し、\(i\) 番目の被験者の \(j\) 番目時点の被説明変数 \(Y_{ij}\) を線形混合効果モデルにて表現すると、以下のようになる。

    $$ Y_{ij}=\beta_1+\beta_2 t_{ij}+b_{1i}+b_{2i}t_{ij}+\epsilon_{ij}\qquad (j=1, 2, \cdots, n_i) $$

    ただし、\(t_{ij}\)は\(i\)番目の被験者の\(j\)番目の(イベント)時点である。以下ではモデルを図で表す。

    1

    2

    3

    固定効果とランダム効果

    線形混合効果モデルは、固定効果（fixed effect）と ランダム効果（random effect）から構成される。

    • 固定効果（fixed effect）: population characteristics shared by all individuals
    • ランダム効果（random effect）: specific effects that are unique to particular individual

    非線形混合効果モデル

    • データが線形モデルで表せない際に用いる。
    • 母集団薬物動態解析、動物の成長曲線等の解析で用いられる。
    • 数式では、以下のように書ける。
    $$ Y_{ij}=f(t_{ij}, \boldsymbol{\beta}, \boldsymbol{b_i})+\epsilon_{ij} $$

    ここで\(\boldsymbol{\beta}\)は 固定効果、\(\boldsymbol{b_i}\)はランダム効果（変量効果）を表すベクトルとした。また、\(f(\cdot)\)は非線形関数であり、データの性状に応じて適切な関数を当てはめる

    引用文献

    • 船渡川伊久子、船渡川隆（2015）統計解析スタンダート　経時データ解析. 朝倉書店.
    • 田中豊、森川敏彦、山中竹春、冨田誠（2008）一般化線形モデル入門（原著第2版）. 共立出版.
    • Scott L. Zeger, Kung-Yee Liang, Paul S. Albert. Models for longitudinal data: a generalized estimating equation approach. Biometrics 1988;44:1049-1060.
    Tags Statistics